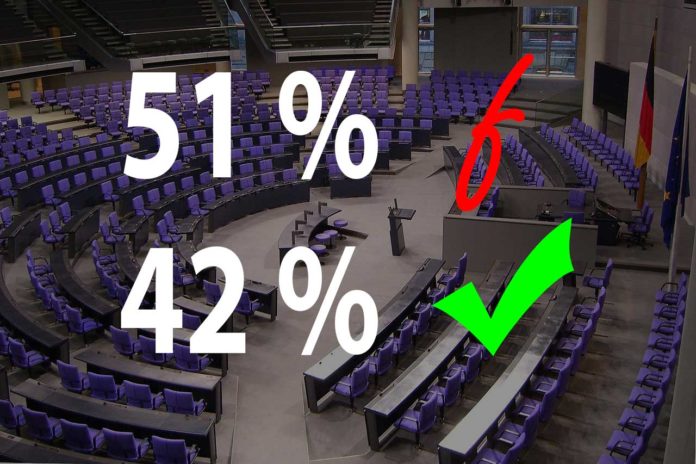
Großes Mißverständnis. Die regierungsfähige Mehrheit liegt NICHT bei 51 %
In letzter Zeit begegne ich zahllosen Menschen, die mir etwas über parlamentarische Mehrheiten, Sperrminorität und einer Chance für die AfD erzählen. In den Sozialen Medien wird immer wieder von möglichen Regierungszusammensetzungen und einer Kanzlerin Alice Weidel geteilt. Gleichzeitig offenbart sich aber auch ein tiefes Unverständnis der Menschen darüber, wie es überhaupt zu Mehrheiten und schlussendlich zur Regierungsbildung kommt.
Angesichts dieses Umstandes frage ich mich immer wieder und wieder, wie Menschen, denen das rudimentärste Basiswissen dazu fehlt, solche Einschätzungen überhaupt tätigen wollen.
Daher hier eine Reihe von unwahren Parlamentsmythen:
1. Die absolute (regierungsfähige) Mehrheit liegt bei 51 %
Nein. Das ist sogar im doppelten Sinne falsch. Wenn man die Mehrheiten an den Stimmenanteilen auf diese Weise berechnen KÖNNTE (Konjunktiv), dann läge sie bei rechnerisch 50,01 %. Aber auch das ist nicht korrekt. Tatsächlich hängen die Stimmenanteile, die man für eine regierungsfähige Mehrheit braucht, von den Stimmenanteilen der „Sonstigen Parteien“ ab. Je mehr Stimmen diese „Sonstigen“ bekommen, desto geringer sind die Stimmenanteile, die man für eine regierungsfähige Mehrheit benötigt.
Sie liegen meist ca. zwischen 40 und 48 %.
Warum ist das so?
Die, für die Parteien angegebenen Stimmenanteile beziehen sich immer auf 100 % der insgesamt abgegebenen Stimmen. Es ziehen aufgrund der 5 %-Hürde jedoch nicht alle Parteien, die Stimmen bekommen haben, in den Bundestag ein. Und nur unter den Stimmen der Parteien, die sich tatsächlich etablieren konnten (also mehr als 5 % oder drei Direktmandate erreicht haben), werden die entsprechenden Mehrheiten in Sitze umgerechnet. Das Ganze geschieht unter Anwendung des Sainte-Laguë/Schepers-Verfahrens in Sitze umgerechnet.
Hier ein Beispiel mit den aktuellsten Umfragewerten unter Einbeziehung des Umstands, dass der Bundestag am Ende 630 Sitze umfassen wird:
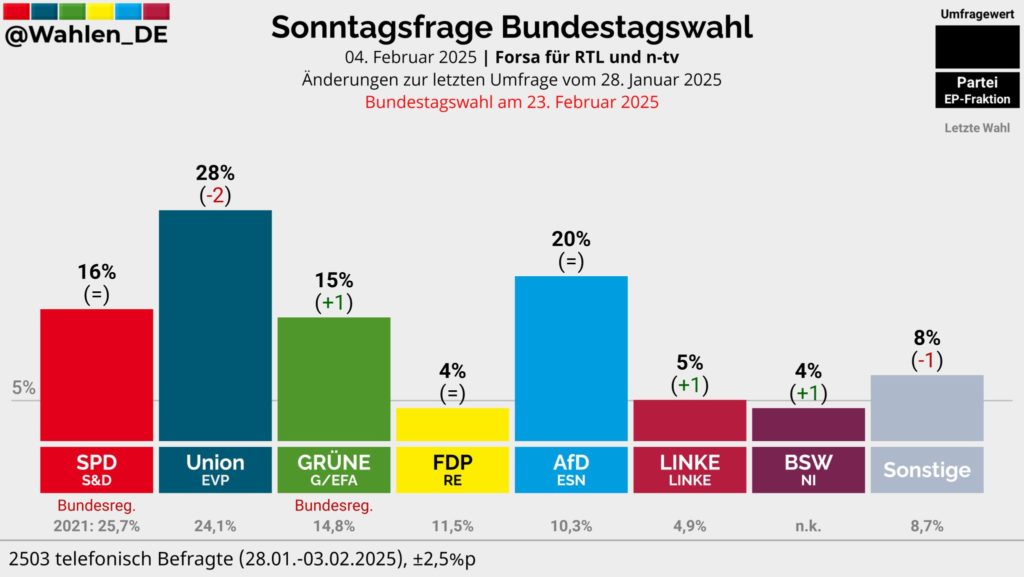
In diesem Fall geht die Berechnung folgendermaßen:

Das bedeutet, dass ca. 42 % (nicht 51 %) eine regierungsfähige Mehrheit ergeben würden.
2. Viele Stimmen bedeuten, dass eine Partei (mit)regieren wird
NEIN! Das war in Deutschland (fast) noch nie so. Selbst nach der allerersten Bundestagswahl 1949 regierte die Union mit der FDP, obwohl die FDP nicht einmal 12 % an Stimmenanteilen und die SPD fast so viele Stimmen wie die Union geholt hatte.
Was viele nicht verstehen ist der Umstand, dass es in Deutschland ein Verhältniswahlrecht gibt und kein Mehrheitswahlrecht. Und dies bei absoluter Koalitionsfreiheit. Wenn eine Partei zwar viele Stimmen holt, aber alleine weder die regierungsfähige Mehrheit auf sich alleine vereint, noch einen Koalitionspartner findet, mit dem diese Mehrheit erreicht wird, dann regiert sie nicht.
Dies ist besonders in Hinblick auf die AfD interessant, die derzeit bei 20 % der Stimmenanteile liegt. Sie ist also noch 22 % von der regierungsfähigen Mehrheit entfernt. Außer der Union gibt es für sie keinen Koalitionspartner, mit der sie koalieren könnte, ohne ihre Glaubwürdigkeit vollends zu verlieren. Würde die Union (entgegen aller Wahrscheinlichkeit) mit der AfD koalieren, würde dies die AfD in eine denkbar schlechte Verhandlungsposition versetzen, da sie keine anderen Optionen besitzt, die Union aber mit SPD und Grünen zwei weitere mögliche Koalitionspartner hat.
Anders wäre es, wenn sich die AfD gezielt einen eigenen Koalitionspartner aufgebaut hätte, oder aber wenigstens eine Partei, welche die Koalitionen zwischen Union, SPD und/oder Grünen verunmöglicht und selber jede Koalition mit diesen Parteien ablehnt. Eine solche Partei wird umgangssprachlich auch als „Blockadepartei“ (nicht zu verwechseln mit einer Blockpartei) bezeichnet. Ihre Wahl erfolgt aus rein strategischen Überlegungen – beispielsweise, um eine schwarz-blaue Koalition zu erzwingen und die AfD dadurch in eine bessere Verhandlungsposition zu versetzen.
Link zu diesem Beitrag
Und ohne Anchor-Tag